Project Summary

Python codes provides a class object to simply calculate quantum mechanical transmission probability across arbitrary potential barriers by using the piece wise constant method. If you have a need to implement transmission probability into your code, it might be helpful.

There are several books and papers describing the piece wise constant method. I referred to specifically a paper by Ando and Itoh [1] along with a paper by Tsu and Esaki [2] and a book by Ferry and Goodnick [3].

Example

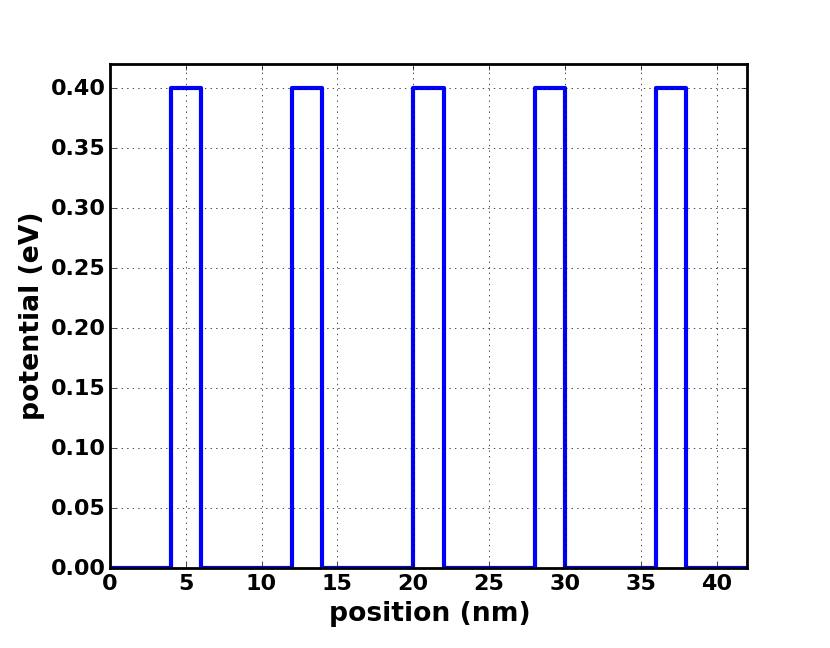
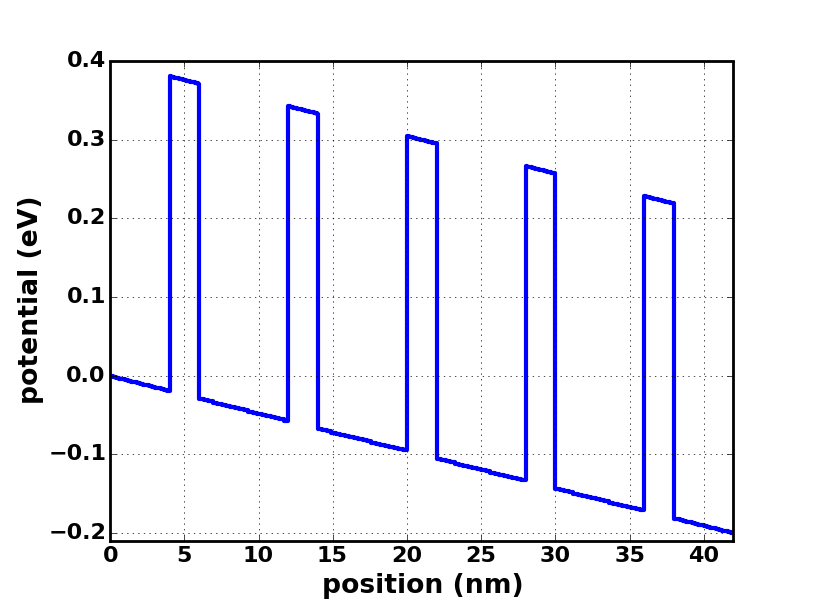
Tunneling through 5 barriers

Potential structure

Biased at -0.2 (V)

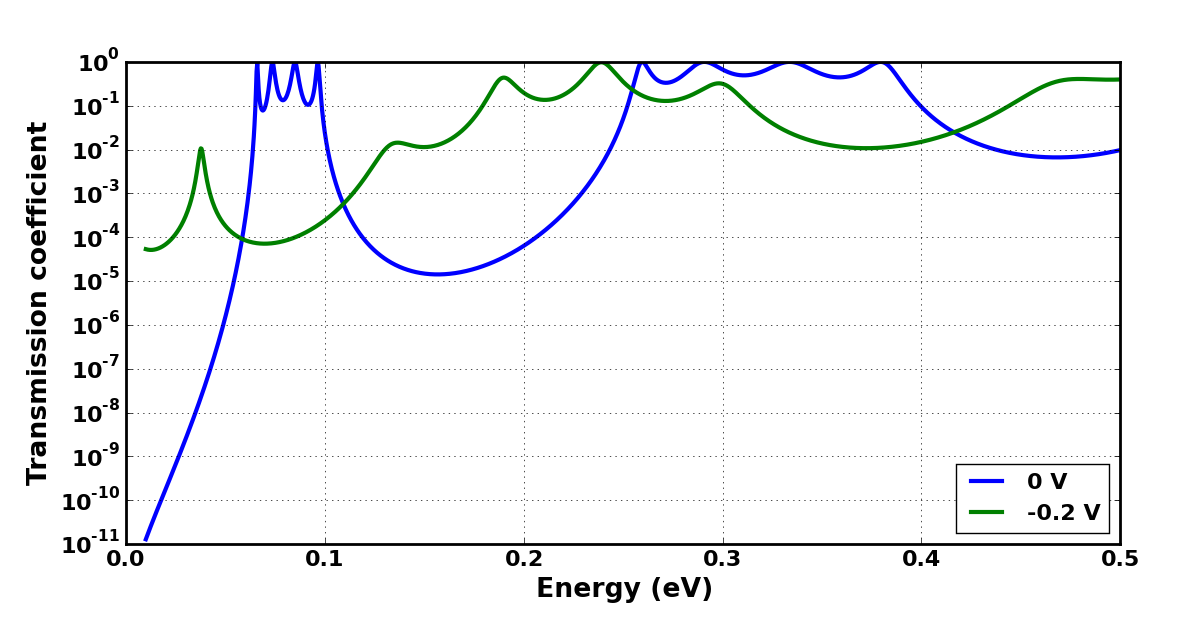
Result:

As can be seen, for 5 barriers without bias, the resonant energies are split into quadruplets. For n barriers, there should be n-1 fold splitting at resonant energies [2].

[1]	Ando, Yuji, and Tomohiro Itoh. “Calculation of transmission tunneling current across arbitrary potential barriers.” Journal of applied physics 61.4 (1987): 1497-1502.

[2]	(1, 2) Tsu, R., and Leo Esaki. “Tunneling in a finite superlattice.” Applied Physics Letters 22.11 (1973): 562-564.

[3]	Ferry, David, and Stephen Marshall Goodnick. Transport in nanostructures. No. 6. Cambridge university press, 1997.

Usage

Set up a desired structure in a separate python module just like below (my5barriers.py for example).

The main part is to set up:

1. potential (eV)
2. thickness (nm)
3. effective_mass (m_0 electron free mass)

# list of effective masses from www.ioffe.ru/SVA/NSM/Semicond/index.html
m = {'GaAs': 0.063,
     'AlxGa1-xAs': lambda x: 0.063+0.083*x,
     'AlAs': 0.146,
     'InN': 0.11,
     'GaN': 0.20,
     'InxGa1-xN': lambda x: 0.2+x*(0.11-0.2),
     'InAs': 0.023}

# Set Up structure Here ---------------------------------------
# potential (eV)
# thickness (nm)
# effective_mass (m_0 electron free mass)
# Multiple Barriers
potential = [0.0, 0.4, 0.0, 0.4, 0.0, 0.4, 0.0, 0.4, 0.0, 0.4, 0.0]
thickness = [4, 2, 6, 2, 6, 2, 6, 2, 6, 2, 4]
effective_mass = [m['GaAs'], m['GaAs'], m['GaAs'], m['GaAs'],
                  m['GaAs'], m['GaAs'], m['GaAs'], m['GaAs'], m['GaAs'],
                  m['GaAs'], m['GaAs']]

Then, in the main module (myTransmissionCoefficient.py), import the module describing the structure ‘as myStr’, e.g.

>>> import my5barriers as myStr

Now create an object

>>> RTD = QuantumTransmissionCoefficientCalculator(20)

The number 20 indicates the subdivision which is useful when applying bias. Check the structure described in the module by

>>> RTD.plot_structure()

Currently, it shows only the potential structure, no effective mass.

Create an numpy array E describing the energy range of interest

>>> import numpy as np
>>> import nu
>>> E = np.linspace(0.01, .5, 1000)*nu.eV

where nu is a custom module dealing with units. In this case, nu.eV = 1.602176565e-19.

Now you can have a transmission coefficient in the desired energy range.

>>> TC = RTD.compute(E)

See Documentation for more details.